Publicidade:

Conjuntos.

Os conjuntos podem ser considerados simplesmente como coleções de objetos.

No início do século XX, porém, quando se tentava formalizar as propriedades dos conjuntos, foram descobertas contradições que afetaram totalmente o pensamento matemático.

Um conjunto pode ser especificado quando se estipulam propriedades que caracterizem seus elementos, ou quando se enumeram seus elementos numa ordem qualquer, sendo indicados por Chaves { }.

Vamos imaginar uma família que possua um gato, um coelho, uma égua, um cachorro, um hamster e um peixe.

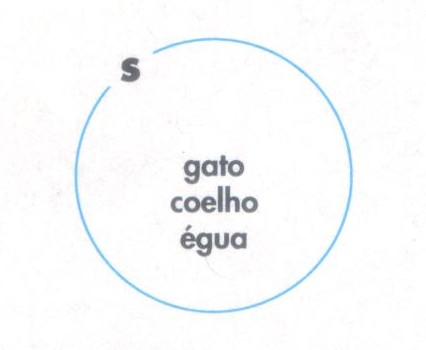
Podemos representar os animais criados por Sara como {gato, coelho, égua] = {x: x animais criados por Sara}.

Conjuntos podem ser representados por um círculo ao redor de seus elementos.

União e Interseção.

Podemos usar os círculos para mostrar a relação entre dois (ou mais) conjuntos.

Suponhamos que Sara tenha um irmão, Tito, que cria o cachorro e o hamster; mas ele também ajuda Sara a cuidar da égua.

Sendo S o conjunto de animais criados por Sara e T, o de animais criados por Tito, é fácil notar que o conjunto de todos os animais criados pelas crianças é {gato, coelho, égua, cachorro, hamster}.

Esse é o conjunto união dos outros dois, escrito como S ∪ T ("S união T"):

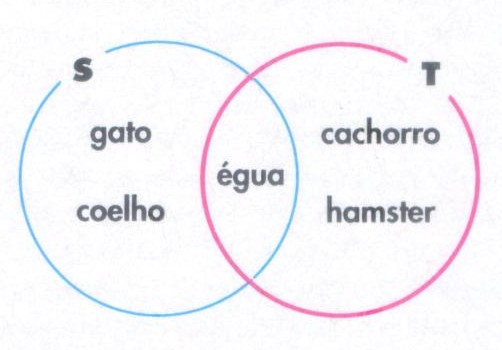
Os conjuntos possuem um elemento em comum, a égua.

O conjunto de elementos que pertencem a dois conjuntos é conhecido como ínterseçâo (representado por ∩); aqui, S ∩ T = {égua}.

Apesar de possuir apenas um elemento, é um conjunto, e escrevemos "égua ∈ {égua}", em que o símbolo ∈ significa "pertence a".

Publicidade:

Subconjuntos.

Um conjunto será subconjunto de outro se todos os elementos do primeiro forem elementos do segundo, ou seja, se um estiver contido no outro.

Neste caso, {égua} é subconjunto de {gato, coelho, égua, cachorro, hamster}.

Se o conjunto maior for A e o subconjunto E, dizemos que E ⊂ A, para indicar que E é subconjunto de A, ou A ⊃ E, para indicar que A contém o conjunto E.

Isto pode ser representado da seguinte forma:

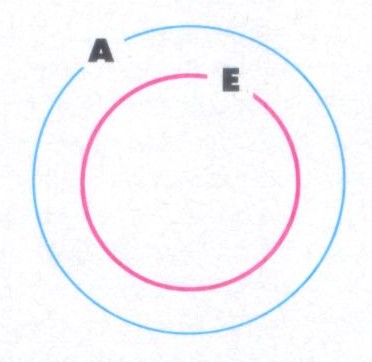
Conjunto Universal e Complementos.

Muitas vezes, precisamos saber quais objetos não pertencem a um conjunto.

Por exemplo, podemos querer saber que animais não são criados por Sara, porém sem incluir todos os outros animais do mundo.

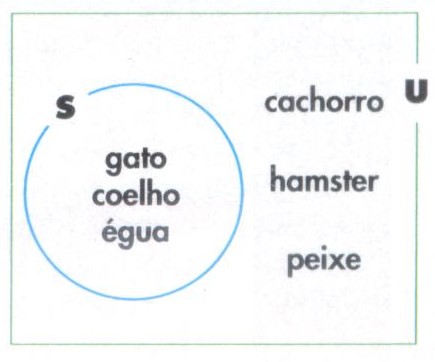
O conjunto universal contém todos os objetos em questão, neste caso, os animais criados pela família, representado pelo retângulo U.

Os animais que não são criados por Sara, dentro do conjunto universal, formam o complemento relativo do conjunto dos animais da menina.

Se S é o conjunto dos animais criados por Sara, seu conjunto complementar é representado como C(S) ou S'.

No caso, S' = {cachorro, hamster, peixe}.

Publicidade:

Conjunto Vazio.

O conjunto vazio (também chamado de conjunto nulo) não possui elementos.

É representado como { } ou Ø.

Se considerarmos a família dos animais, podemos escrever:

{animais dos pais} ∩ {animais de Sara} = Ø

Para indicar que o conjunto formado pelos animais criados por Sara e pelos animais criados por seus pais é um conjunto vazio.

Conjuntos Disjuntos.

Conjuntos disjuntos são os que não possuem elementos em comum.

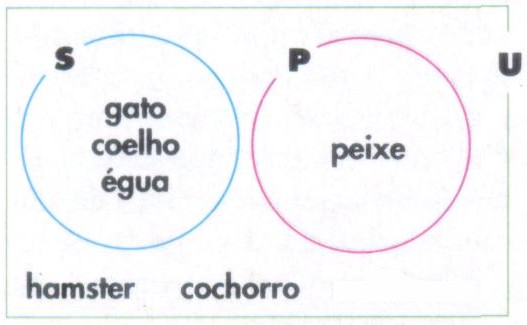
Como mostra o diagrama abaixo, o conjunto dos animais criados por Sara não tem interseção com o conjunto P, dos animais criados por seus pais.

S e P não possuem elementos em comum e sua interseção é o conjunto vazio.

Ou seja, S ∩ P = Ø

Acesse nossos Exercícios Grátis.
Adição
Subtração
Multiplicação
Divisão

Conjuntos e Lógica.

Existe um vínculo direto entre a teoria dos conjuntos e a lógica, que se torna evidente quando representamos as definições formais de união, interseção e complemento através da notação dos conjuntos:

S ∪ T = {x: x pertence a S ou a T}

S ∩ T = {x: x pertence a S e a T}

S’ = {x: x não pertence a S}

Os termos "e", "ou" e "não" representam o que os lógicos chamam de funções-verdade.

Isto significa que quando se encontram ligadas a sentenças formando sentenças mais complexas, a verdade ou falsidade do último depende apenas do precedente.

Por exemplo, a afirmação "João está em Londres e Maria, em Paris" só pode ser verdadeira se ambas as afirmações, "João está em Londres" e "Maria está em Paris", forem individualmente verdadeiras.

Neste caso, "João não está em Londres" deve ser falsa.

Estas relações podem ser demonstradas por meio da seguinte tabela:

Onde P e Q representam sentenças quaisquer, "-P" é "não-P", "P & Q" é lido como "P e Q" e "P v Q" representa “P ou Q".

A tabela mostra todas as combinações possíveis e pode ser usada como preparação para fórmulas mais elaboradas.

Quando "V" representa um sinal positivo e "F", a ausência deste (às vezes representados respectivamente como "1" ou "0"), esta tabela mostra as saídas de portões lógicos eletrônicos de mesmo nome a partir dos quais são construídos os computadores.

Gottlob Frege.

Gottlob Frege foi juntamente com Bertrand Russell o fundador da matemática lógica.

Frege publicou muitos trabalhos de caráter filosófico sobre matemática.

Ele afirmava que "Todo bom matemático é meio filósofo e todo bom filósofo é meio matemático".

Paradoxos.

Embora os desenvolvimentos do simples conceito de conjunto, como os apresentados, pareçam funcionar bem para finalidades de ordem prática, vários paradoxos foram descobertos quando se buscavam axíomas para a teoria dos conjuntos.

O alemão Gottlob Frege (1848-1925) e o inglês Bertrand Russell (1872-1970) desejavam demonstrar que toda a matemática podia ser reduzida a pura lógica e se voltaram para a teoria dos conjuntos para estabelecer esse elo.

Em 1908, exatamente quando Frege publicava relevante trabalho sobre o assunto, Russell descobriu e comunicou a Frege que seus axiomas geravam importante contradição, que se tornou conhecida como paradoxo de Russell.

A maneira mais simples de explicar o paradoxo de Russell é através de um exemplo específico.

Consideremos um médico que atende uma comunidade e só trata das pessoas que não tratam de si mesmas.

Se o médico trata de si mesmo, ele não pode ser incluído no conjunto das pessoas que não tratam de si mesmas.

Se ele não trata de si mesmo, então está incluído no conjunto daqueles que ele trata.

De uma maneira ou de outra, existe uma contradição; só há duas possibilidades e nenhuma das duas faz sentido completamente.

Deve haver algo de errado com a própria definição, que permite derivar dela uma contradição.

Este e outros paradoxos se constituíram num grande revés para os lógicos matemáticos e novas filosofias, como o intuicionismo, surgiram em parte como consequência disso.

O Paradoxo de Russell.

É óbvio que os conjuntos em geral podem pertencer a outros conjuntos; por exemplo:

{1,2} é elemento de {{0,1 }, {1,2}, {2,3}}... e este conjunto é elemento do conjunto de conjuntos de três elementos que, por sua vez, pertence ao conjunto dos conjuntos maiores (já que há muitos conjuntos de três elementos).

Mais especificamente, alguns conjuntos são elementos de si mesmos, como o conjunto dos conjuntos grandes, enquanto outros não são elementos deles mesmos, como o conjunto dos conjuntos pequenos (já que há muitos conjuntos pequenos).

Consideremos o conjunto W de todos os conjuntos que não são elementos de si mesmos: é ele elemento de si mesmo ou não?

Um elemento de um conjunto precisa ter a propriedade que define o conjunto.

Assim, se W é elemento do conjunto dos conjuntos que não são elementos deles mesmos, não pode ser elemento de si mesmo, mas isto signifîca exatamente que ele não pode ser elemento de W.

Por outro lado, se W não é elemento de si mesmo, trata­se exatamente da propriedade que define W, de modo que W precisa ser elemento de W, ou seja, é elemento de si mesmo.

Existem duas possibilidades:

Se pensarmos em alguma coisa de que gostamos e em um conjunto qualquer de que gastamos, ou a coisa está no conjunto ou não; não há uma terceira possibilidade.

Assim, neste caso, ou W é elemento de si mesmo ou não é, ainda assim, qualquer que seja a suposição que fizermos, somos levados diretamente à contradição.

Este é um problema profundo que o paradoxo descrito anteriormente, embora a descrição da situação do médico pareça inofensiva, a análise mostra que ela é realmente autocontraditória.

Aqui não há tal descrição para rejeitar; W foi construído a partir da lógica pura.

A contradição, pois, só pode estar em um lugar, no cerne da própria lógica.

Conteúdo Relacionado.

Ondulatória
Acústica
Ótica
Matemática e Suas Aplicações
Matemáticos Importantes
Álgebra Booleana, Operadores Booleanos
A Teoria do Caos, Efeito Borboleta
Sistemas Numéricos
Notações Numéricas
Movimento e Força
Sir Isaac Newton
Calor e Energia
Forças Que Afetam Sólidos e Fluidos
Transferência de Calor
Átomos
Conjuntos
Corrente Elétrica